The churn is a phenomenon in which customer stop doing business with an entity. It is most commonly expressed as the percentage at which subscribers discontinue their subscriptions within a given time period. Churn can be applied to subscription-based businesses as well to the number of employees that leave a firm. The churn rate and growth rate are diametrically opposite factors, as the former measures the loss of customers and the other measures the acquisition of customers. It is therefore, one of the fundamental use cases companies seek to implement.
Now-a-days, machine learning models provide the most affective means to measure, understand and predict customer churn. This blog is one such effort in this direction and will help you with in the follows ways:
- How to formulate the problem.
- Use of XGBoost to predict customer churn.
- Use of custom loss function
- How to estimate model efficacy.
Data Acquisition & Wrangling
The data used in this study is taken from Kaggle, published under the name Bank Customer Churn Prediction. All the rights are owned by the original publisher. The data is easy to understand with just 1000 rows and 14 columns. I.e.,
| RowNumber | CustomerId | Surname | CreditScore | Geography | Gender | Age | Tenure | Balance | NumOfProducts | HasCrCard | IsActiveMember | EstimatedSalary | Exited |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 15634602 | Hargrave | 619 | France | Female | 42 | 2 | 0 | 1 | 1 | 1 | 101348.88 | 1 |
| 2 | 15647311 | Hill | 608 | Spain | Female | 41 | 1 | 83807.86 | 1 | 0 | 1 | 112542.58 | 0 |
| 3 | 15619304 | Onio | 502 | France | Female | 42 | 8 | 159660.80 | 3 | 1 | 0 | 113931.57 | 1 |
There are no null values within therefore, no need to fill NAs. We dropped the useless columns, use 'Exited' as the target variable and perform label encoding to convert categorical variables into integers so that they can be passed to XGBoost train function. This is done in a very few lines as follows:
### Let us now build the X and y variables
df_y = df['Exited']
df_x = df.drop(['RowNumber', 'CustomerId', 'Surname', 'Exited'], axis=1) # droping the useless columns
columns=df_x.columns
for f in df_x.columns:
if df_x[f].dtype == 'object':
df_x[f] = LabelEncoder().fit_transform(list(df_x[f]))
We have the problem of unbalanced classes here for which we will be using class weights explicitly, calculated as follows:
class_labels = np.unique(df_y)
class_weights = class_weight.compute_class_weight(class_weight='balanced', classes=class_labels, y=df_y)
class_weights = dict(zip(class_labels, class_weights))
class_weights
{0: 0.6279040562602034, 1: 2.454590083456063}
The above function gives a clear indication of class imbalances. One way to deal with such a problem is via using custom loss function which put different emphasis on classes w.r.t their weights. Focal loss function is exact such function explained below.
Focal Loss Function
Here, we implemented a custom loss function namely, Focal Loss. It provides an improvement over Cross-Entropy Loss (CE) and handles the problem of class imbalance better by assigning more weights to hard or easily misclassified examples and to down-weight easy examples. See more detail about Focal Loss here.
def focal_loss_lgb_eval_error(y_pred, dtrain, alpha, gamma):
a,g = alpha, gamma
y_true = dtrain.label
p = 1/(1+np.exp(-y_pred))
loss = -( a*y_true + (1-a)*(1-y_true) ) * (( 1 - ( y_true*p + (1-y_true)*(1-p)) )**g)
* ( y_true*np.log(p)+(1-y_true)*np.log(1-p) )
# (eval_name, eval_result, is_higher_better)
return 'focal_loss', np.mean(loss), False
focal_loss_eval = lambda x,y: focal_loss_lgb_eval_error(x, y, alpha=0.25, gamma=1.)
Model Train and Validation
For the sake of simplicity, we have used only the following few parameters which are als the main parameters of XGBoost sufficient enough to achieve good results.
params = {'max_depth': 100
,'num_leaves': 10
,'learning_rate': 0.01
,'max_bin': 100
,'objective': 'binary', 'verbose':-1
}
num_boost_round=10000
train_auc_list = []
valid_auc_list = []
early_stopping_rounds = 50
Here we have used StratifiedKFold cross validation using 3-folds with a train/test split of 70/30. Both sigmoid and f1_score functions can be custom build or used from sklearn.
num_boost_round=10000
train_auc_list = []
valid_auc_list = []
early_stopping_rounds = 50
### let's do 70/30 split
df_X_sub, X_test, df_y_sub, y_test = train_test_split(df_x, df_y, test_size=0.33, random_state=42)
cv = StratifiedKFold(n_splits=3, shuffle=True, random_state=42)
for train_index, test_index in cv.split(df_X_sub, df_y_sub):
X_train, X_valid = df_X_sub.loc[df_X_sub.index[train_index]], df_X_sub.loc[df_X_sub.index[test_index]]
y_train, y_valid = df_y_sub.loc[df_y_sub.index[train_index]], df_y_sub.loc[df_y_sub.index[test_index]]
train_data = lgb.Dataset(data=X_train, label=y_train,
categorical_feature=categorical_feature,
free_raw_data=False)
valid_data = lgb.Dataset(X_valid, label=y_valid,
categorical_feature=categorical_feature,
free_raw_data=False)
evals_results = {}
model_lgb = lgb.train(params,
train_data,
valid_sets=valid_data,
evals_result=evals_results,
num_boost_round=num_boost_round,
#early_stopping_rounds=early_stopping_rounds,
verbose_eval=None,
feval=focal_loss_eval
)
train_preds = sigmoid(model_lgb.predict(X_train))
train_binary_preds = [int(p>0.5) for p in train_preds]
valid_preds = sigmoid(model_lgb.predict(X_valid))
valid_binary_preds = [int(p>0.5) for p in valid_preds]
train_auc = f1_score(y_train, train_binary_preds)
valid_auc = f1_score(y_valid, valid_binary_preds)
train_auc_list.append(train_auc)
valid_auc_list.append(valid_auc)
print(np.mean(train_auc_list))
print(np.mean(valid_auc_list))
As it can be seen that the function is highly customized, i.e., developer has the a huge freedom insert his/her hocks (change the probability thresholds right in the training process), change loss function and can calculate the model performance between train and validation sets separately ( note that validation set is not test set). This is a very convenient way to catch any over-fitting, i.e., if considerable difference between train and validation results are observed, drop the iteration. Since we are observing results from a pre-defined parameter set, the benefits of such an approach are not obvious, but we hope that this point will be even better understood in our coming blogs where a hyper-parameter search is used to further improve the prediction results.
Once the train and validation results are verified using several-fold cross validation, next step is to fit the model on the selected paramters as follows:
model_lgb = lgb.LGBMClassifier(**params, class_weight = class_weights).fit(df_X_sub, df_y_sub)
Perform Evaluation
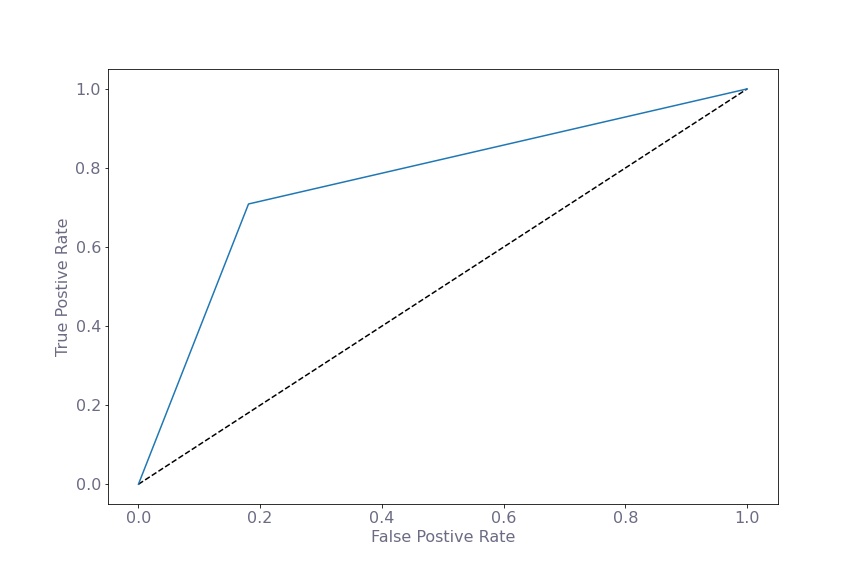
Next we measure the train and test results. Since we are dealing with unbalanced class problem here, the metric of our interest is F1-Score and Area Under the Curve (AUC)
clf_train_pred = model_lgb.predict(df_X_sub)
clf_test_pred = model_lgb.predict(X_test)
The train and test AUCs are 76.9% and 76.3% respectively and ensures that there is no over-fitting. F1 Scores are 58% and 56% respectively.
Additional evaluation metrics are as follows:
| precision | recall | f1-score | |
|---|---|---|---|
| 0 | 0.92 | 0.8 | 0.85 |
| 1 | 0.49 | 0.74 | 0.59 |
| accuracy | 0.78 | ||
| macro avg | 0.71 | 0.77 | 0.72 |
| weighted avg | 0.83 | 0.78 | 0.80 |
An overall 58% F1-score of such an imbalance dataset is not bad performance at all. We have however not used any hyper-parameter optimization approach which can drastically improve the final results. Please stay tune to read our next post on various hyper-parameter tuning approaches.
Leave a Comment
Your email address will not be published.